Gibbsova voľná energia
Je to iba definičný vzťah, taká skratka
Samovoľné deje vždy prebiehaju s klesajúcou Gibsovou energiou $\Delta G < 0$
$\Delta_rG < 0 \implies \to$ , reakcia ku produktom
$\Delta_rG < 0 \implies \leftarrow$ , reakcia ku reaktantom
$\Delta G = \text{zmena voľnej Gibsovej energie}$
$\Delta H = \text{zmena entalpie}$
$T = \text{teplota v Kelvin}$
$\Delta S = \text{zmena entropie}$
$$\Delta G = \Delta H - T\Delta S$$
$$\Delta G = -RT\ ln\ K_{C}$$
$$ \Delta_rG=\Delta_rG^o + RT\ln(\prod a_i^{v_i}) = \Delta_rG^o + RT\ln Q \qquad a_i=\frac{p_i}{p^o} \lor \frac{c_i}{c^o} $$
$$Q = \prod_ia_i^{v_i} = \frac{a_P^{v_P}a_R^{v_R}}{a_A^{v_A}a_B^{v_B}} \qquad \lim_{t \to \infty} Q \to K \ \text{ (rovnovážna k.)} $$
Pri konštantnej teplote:
$$\Delta_rG=RT\ln\frac{Q}{K}$$
# Entropia
Pri vyšších teplotách sa uprednostňujú produkty s vysokou entropiou
-> uprednostňujú sa reakcie kde $n_r < n_p \implies \sum \nu_i > 0$
# Aktivačné energie
Rozdiel energie medzi reaktantom a prechodným stavom
Prechodný stav:
Reprezentuje energetické maximum, hocijaký posun vedie k stabilnejšiemu produktu
Nedá sa izolovať
Arhéniova rovnica:
Aktivačná energia určuje rýchlosť reakcie, pričom energia látok nadobúda Gausovú distribúciu
$$k=Ae^{-E_a/RT}\qquad r=k*[A]*[B]$$
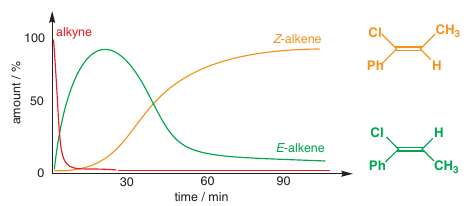
# Kinetická a termodynamická kontrola
Výsledok reakcie:
kinetická kontrola -> záleží na relatívnej enerii prechodných stavov ku produktom
termodynamická kontrola -> záleží na pozícii rovnováhy (stabilite/energii produktov)

# Prvý zákon termodynamiky
$$\Delta U=q+w \qquad \text{q - teplo, w - práca}$$
$$\Delta U=\Delta H-p\Delta V \implies \Delta H=\Delta U+p\Delta V$$
Entalpia < 0 -> exotermický proces - teplo sa uvoľňuje z väzieb
Entalpia > 0 -> endotermický proces - teplo sa ukladá do väzieb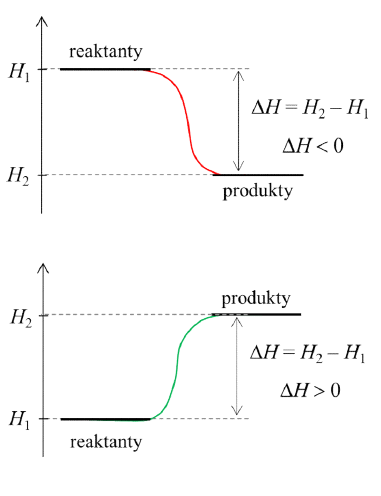
Čím je $\Delta H_r$ zápornejšia, tým je látka stabilnejšia
# Reakčné entalpie
$$\Delta_r H^0=\sum_i\Delta_f H^0_i$$
Entalpia reakcie = súčet tvorných entalpií produktov - súčet tvorných entalpií reaktantov